La mejor fórmula matemática para cortar una pizza

Llegó la hora de sentarse a la mesa. Toca repartir un pizza entre cuatro hambrientos comensales que no están dispuestos a perdonar ni un solo gramo de la ración que les corresponde. Pero muchas veces hay un problema. Que el encargado de dividir el alimento en cuatro partes no tiene la precisión de un cirujano y acaba sacando cuatro trozos de muy distinto tamaño. Da igual que se emplee un cuchillo, la siempre tan socorrida tijera o el utensilio específico que hay en muchas cocinas y que actúa como una radial sobre la masa recién salida de un horno; al final, el resultado, siempre es muy similar.

Con pocos a repartir suele bastar un poco de puntería y sentido común para acabar con unas porciones relativamente parecidas. Sin embargo, cuando se trata de distribuir entre más comensales, el asunto empieza a complicarse.

Un equipo de matemáticos de la Universidad de Liverpool (Reino Unido) se ha decidido ha ponerle freno a semejante injusticia. Para ello, han desarrollado un sistema basado en los principios de la geometría más elementales.

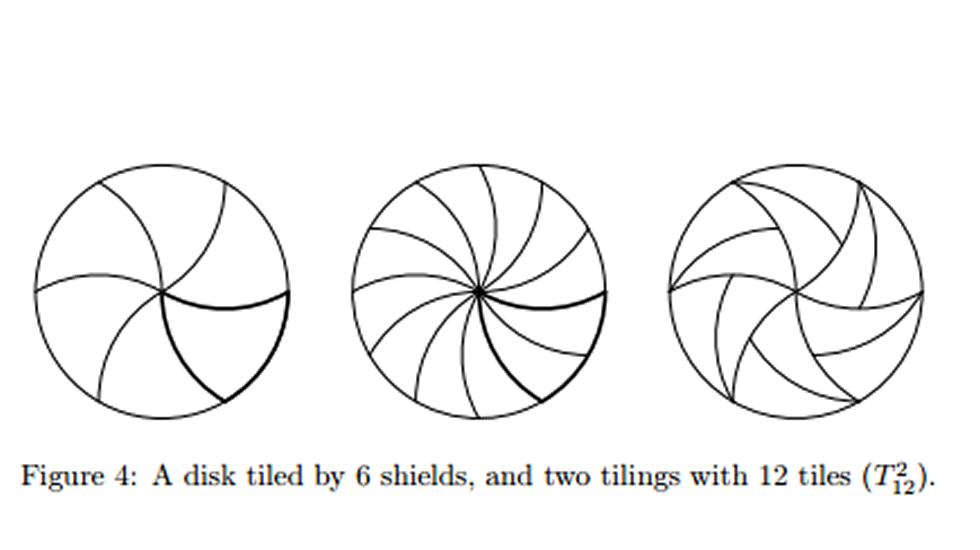
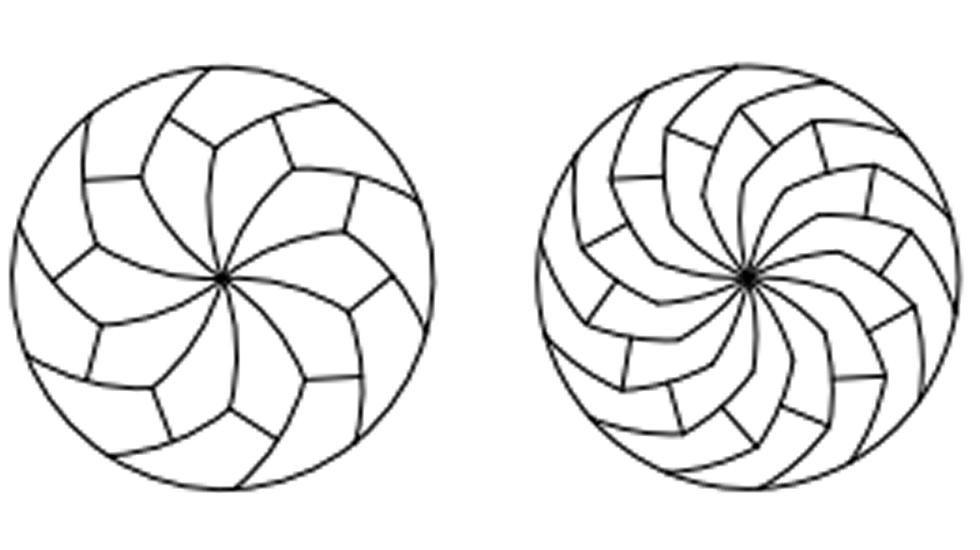
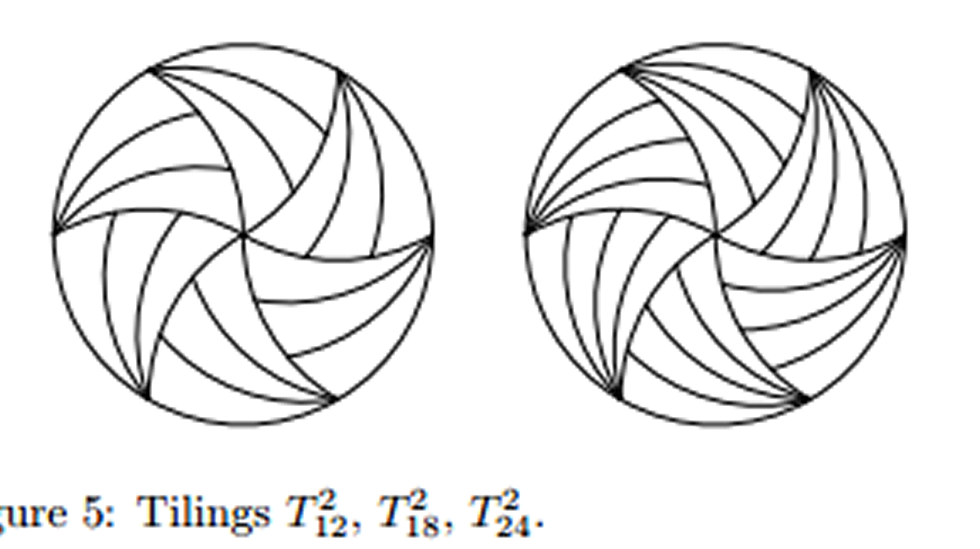
En una de sus publicaciones científicas demuestran cómo repartir una pizza en 12 porciones idénticas. Para entenderlo conviene apoyarse en la ilustración que acompaña a la información. En primer lugar, cortar la base en seis trozos iguales curvos (figura 1), y cada uno de estos, a su vez, dividirlos por la mitad, también a través de un corte curvo (figuras 2 y 3).

Con este método de Haddley y Worsley, siempre y cuando se corta la pizza en porciones con forma con la forma de la hoja de una guadaña y existan un número impar de lados, «cada una de estas rebanadas pueden seguir subdividiéndose hasta el infinito», aseguran en el diario británico The Independent. «No hay límite».